Simple Continued Fraction Expansion of Pi

Show me some pictures!

Back in the 1960s, the L.W. Singer Company (Random House) put out a series of books, aimed at high school students, called the New Mathematical Library. Amongst some two dozen titles, there was Ivan Niven's Numbers: Rational and Irrational, as well as his Mathematics of Choice, P.J. Davis' The Lore of Large Numbers, Oystein Ore's Invitation to Number Theory, Ross Honsberger's marvelous Ingenuity in Mathematics, and C.D. Olds' Continued Fractions.

It was this last title that taught me the some basics about continued fractions - numbers written in the form: a0 + b1/(a1 + b2/(a2 + b3/(a3 + ...))). In "simple" continued fractions, all the b's are 1 and the number can be re-written as [a0; a1, a2, a3, ...]. In the book it was noted that pi = [3; 7, 15, 1, 292, 1, 1, ...]. Taking just the first four terms, we can approximate pi to 3 + 1/(7 + 1/(15 + 1/1)) = 3 + 1/(7 + 1/16) = 3 + 1/(113/16) = 3 + 16/113 = 355/113. This is an excellent approximation and was known to (Chinese mathematician) Zu Chongzhi prior to 500 A.D. Europeans would not make mention of this fraction for another 1000 years!

One of the interesting things about the continued-fraction expansion of (irrational) numbers is that they are, in a sense, base-independent. Instead of endlessly repeating digits of the base in which we are representing the number (digits 0 - 9 in base ten), we get "whole" numbers: 1, 2, 3, etc. - as large as you wish. So we find a relatively large "292" fairly early in the simple continued fraction form of pi. What other large numbers might there be? How common are they?

C.D. Olds actually gave 23 terms of the simple continued fraction expansion of pi and, in late 1984, I complained about this (paucity of data) to Martin Gardner, then mathematical-games columnist for Scientific American. Mr. Gardner let me know that a Bill Gosper had calculated many thousands such terms and was kind enough to supply me with Mr. Gosper's address.

Bill Gosper was one of the authors of HAKMEM. I had heard of him because of his discovery of the first glider-gun in Conway's remarkable "game of life". On Friday, 19 August 1977 he had a computer churn out 204,103 terms of the simple continued fraction form of pi. When I asked him for a copy, he was kind enough to mail me a XEROX of the 205-page printout.

For the next few years I went over the print-out, sifting out (for instance) the first occurrences of numbers and trying to quantify the relative frequencies of their occurrences. [A. Ya. Khinchin wrote a Continued Fractions book in 1935 that was not, alas, translated into English until 1961. In it he works out the theory for number-occurrence frequencies.] It was difficult work and I soon tired of it - recognizing that one day all of this might be much more easily had by way of a "personal" computer.

In 1985, Bill Gosper went on to calculate 17,001,303 terms of the simple continued fraction expansion of pi. Of course others were pushing the number of decimal-digits known of pi toward the billion-places mark but, even though these attempts often made the media, I was unimpressed. By 1995, I was able to calculate only a measly 10000 terms of the number using Mathematica on my old Macintosh. Lack of adequate memory was the major impediment to progress. That year I looked up Bill Gosper's e-mail and asked for an electronic version of his calculations. He replied: "I just lost a disk with 17000000. When I get a new one, we'll see how well my old backup tapes work."

When Mathematica 4 came out in May 1999, I immediately ordered my upgrade. Incredibly, they had incorporated the ContinuedFraction function into the body of the program (it used to reside in an add-on package) and, on my first try, I was able to come up with 10 million terms (of pi) on my G3/300/384. Next I calculated 17 million. Finally, playing with assorted larger values, I managed to get 20 million terms without running out of memory. The calculation took 6 hours and resulted in a 62 MB output file. Simon Plouffe of Plouffe's Inverter believed the 20 million terms were a record and was kind enough to give them web-space, although that link has not been operational for a while.

One year later, a RAM doubling allowed me to calculate 40 million terms. And, in October 2000, an iMac DV equipped with a GigaByte of RAM churned out 53 million terms in under 20 hours. [The critical MathKernel registered at 976.6 MB. An attempt to run the MathKernel in OS X Beta (under "Classic" environment), where it registered at over 990 MB, proved inconsequential in finding more terms.]

Let [0; 1, 2, 3, 4, 5, ...] represent the indices of the continued fraction terms [3; 7, 15, 1, 292, 1, ...], or (better, perhaps) think of the terms as having dropped the initial '3'. Then the "first occurrence indices" of the positive integers are: {3, 8, 10, 29, 39, 31, 1, 43, 129, 99, ...}. A full 3131 terms of this sequence is given here. It is a trivial variation of Sloane's A032523.

Of course, every integer is not just expected to show up once, but an unlimited number of times. So I have devised a somewhat accelerated sequence: The "n-th occurrence indices" of the positive integers (i.e., the first occurrence of '1', the second occurrence of '2', the third occurrence of '3', etc.): {3, 13, 38, 87, 188, 192, 145, 616, 857, 873, ...}. A full 421 terms of this sequence is here.

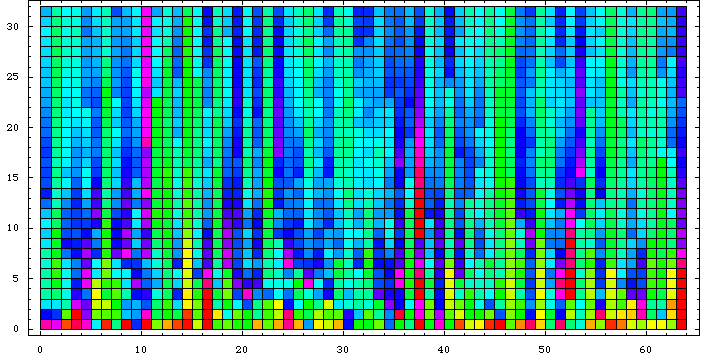
A picture of the ratio of the first 32 occurrences of the first 64 numbers to their "expected" values:

Well, this is just a "fingerprint" of sorts. One may do it differently by computing the geometric mean of a given number of terms (up to 20000, in this case) and subtracting Khinchin's constant:

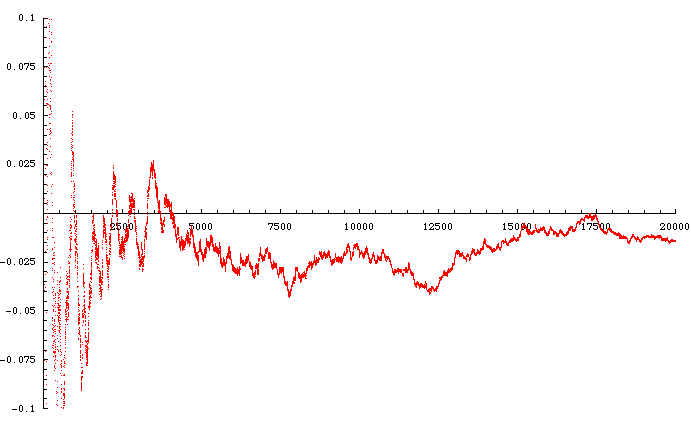
Here's a close-up of that approach to the axis just prior to 17500:

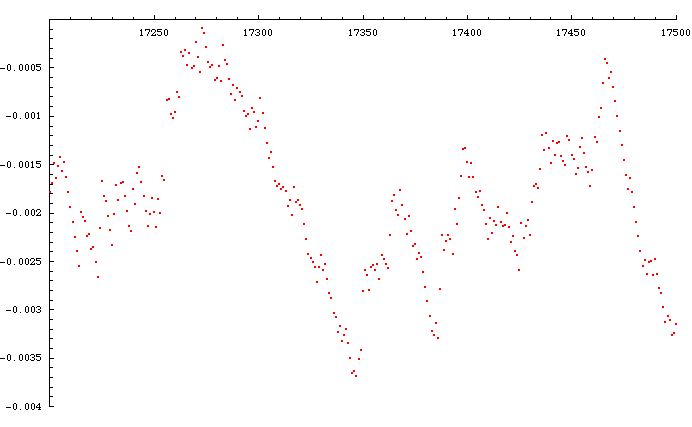
The value of the reduced geometric mean at 17273 is -0.0000910381. We actually got closer to the axis at 976 already, where the value was only -0.00000642897. The list of progressively closer approaches to the axis comprises a pi Khinchin-approach sequence: {1, 3, 7, 8, 9, 10, 11, 15, 16, 17, 97, 100, 103, 117, 976, 32307, 32760, 32787, 60508, 60601, 60663, 187154, 230084, 1120375, 1146529, 2211732, 4497058, ...}. Let's have a look at the geometric-mean neighbourhood of that last point:

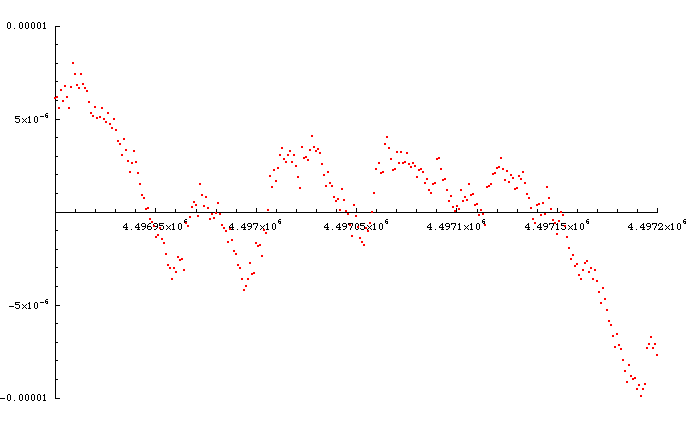
The value of the reduced geometric mean at 4497058 is 0.000000000170948. The next point that comes even closer to Khinchin's constant must be greater than 53 million. At 53000000, the value of the reduced geometric mean is 0.000632746.