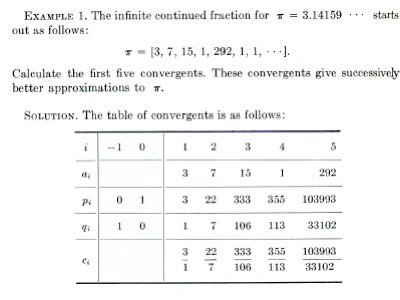
The scan is from C.D. Olds' 1961 Continued Fractions (page 58). There he gives the start of the infinite continued fraction π = [3; 7, 15, 1, 292, 1, 1, ...]. I replaced his comma after the 3 with a semicolon. This (to me) is rather important, because when one calculates a geometric mean of continued-fraction terms, the integer part (term #0, in this case 3) should not be included. (If it were, numbers between 0 and 1 would have a geometric mean of zero.) A geometric mean is very useful in understanding the terms of an infinite continued fraction (lots of 1s, fewer 2s, fewer 3s, etc., but no number is excluded — in fact, we expect every positive integer to appear, sooner or later). So, right off the bat, we have 7, 15, and 292 making a show, which makes gawking at 53 million continued-fraction terms a helluvalot more pleasurable than examining 5 trillion decimal digits.

The 53 million terms Mathematica calculated for me back in October 2000 were surpassed in March 2002 by 180 million terms. As far as I am aware, this is still the record.

Addendum: A record broken