Infinite Squares

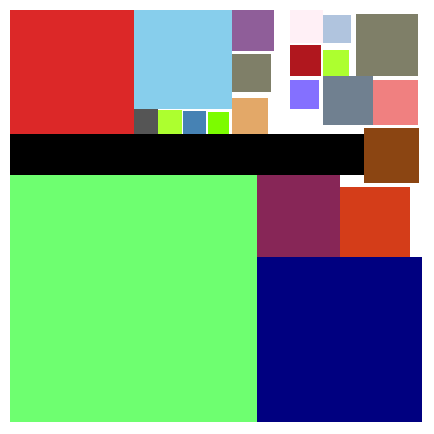
Can you fit the infinite set of squares, with sides of length {1/2, 1/3,
1/4, 1/5, 1/6, 1/7, ...}, into a square of length 5/6?

Mathematical Carnival: Mrs. Perkins' Quilt and Other Square-Packing Problems.
Gardner references a 1967 paper by Moser & Moon and notes a diagram is
available in Moser & Meier's "On Packing of Squares and Cubes" [Journal of
Combinatorial Theory, September 1968].

Kevin Wald writes:

Well, I don't know if it's the same proof given there, but here's one way to
fit them all in that I figured out a while back (to save time, in what
follows I'll refer to the square of side 1/n as "square n"):

First of all, note that squares 24 and higher can all be put into a rectangle
of height 1/12 and length 43/60, as follows: Divide the rectangle into
infinitely many horizontal stripes of height 1/24, 1/48, 1/96, etc.
Squares 24-47 go into the first stripe, 48-95 into the second, 96-191 into
the third, etc. (This is very much like the technique described in Gardner's
book for fitting all the squares into the 1-by-1 square.)

We can now fit squares 2-23 and this rectangle into the 5/6-by-5/6 square if
we put their lower left-hand corners at the following coordinates, measured
in units of 1/60 (so we are attempting to fit them all into the square with
corners (0, 0), (0, 50), (50, 50), and (50, 0)):

2: 0,0; 3: 30,0; 4: 0,35; 5: 15,38; 6: 30,20; 7: 40,20; 8: 42,42; 9: 43,29;
10: 38,36; 11: 44,36; 12: 27,45; 13: 27,40; 14: 27,35; 15: 34,46; 16: 34,42;
17: 34,38; 18: 38,46; 19: 38,42; 20: 15,35; 21: 18,35; 22: 21,35; 23: 24,35;
rectangle: 0,30.

(If you draw it on graph paper, you'll see that this makes all the squares
and the rectangle fit, even if you round all the square sizes up to the
nearest 1/60.)


To generate this picture in Mathematica...

<< Graphics`

wald = {{0, 0}, {30, 0}, {0, 35}, {15, 38}, {30, 20}, {40, 20}, {42, 42},{43, 29}, {38, 36}, {44, 36}, {27, 45},

{27, 40}, {27, 35}, {34, 46}, {34, 42}, {34, 38}, {38, 46}, {38, 42}, {15, 35}, {18, 35}, {21, 35}, {24, 35}};

sw = wald/60;

ne = Table[sw[[i]] + 1/(i + 1), {i, 1, 22}];

sq = Table[{sw[[i]], ne[[i]]}, {i, 1, 22}];

Show[Graphics[Flatten[Append[Table[{ToExpression[AllColors[[Random[Integer, {1, 193}]]]],

Rectangle[First[sq[[i]]], Last[sq[[i]]]]}, {i, 1, 22}],

{Black, Rectangle[{0, 1/2}, {43/60, 1/2 + 1/12}]}]]], AspectRatio -> Automatic]

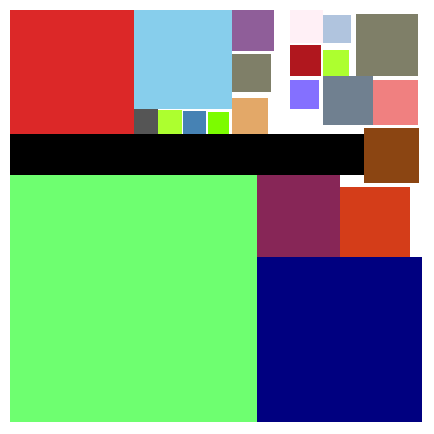
And here is a magnification that black rectangle, filled with the first three layers of (24+48+96) squares:

All colors in these pictures were randomly selected from the set of 193 available "named" colors in the Mathematica add-on "AllColors" function. For a listing of all but one of these, see my "What's missing..." puzzle.]