Antipodal Map Intersections

New Zealand

There was (and perhaps still, is) a bit of trivia floating around suggesting that an antipodal map of New Zealand corresponds (roughly) with Italy. Here, I implied otherwise.

Well, I finally got around to attempting antipodal map illustration in Mathematica...

<< Miscellaneous`WorldPlot`

<< Graphics`Colors`

Bear in mind that Mathematica's polygonal representation of countries is extremely crude:

World[[113]]

WorldData[%]

"New Zealand"

{{{-2501, 10441}, {-2430, 10363}, {-2505, 10288}, {-2773, 10004}, {-2753, 10247}, {-2685, 10229}, {-2634, 10332}, {-2598, 10257}, {-2596, 10365}, {-2501, 10441}}, {{-2381, 10616}, {-2497, 10514}, {-2412, 10521}, {-2365, 10428}, {-2224, 10497}, {-2065, 10362}, {-2258, 10560}, {-2262, 10713}, {-2381, 10616}}}

All coordinates are in minutes of arc. North [+] and south [-] latitudes (the first term of each pair) are simple enough to invert. East [+] and west [-] longitudes require a little more fiddling. Starting with a specific transformation of the above, I eventually hacked my way to a more generalized coding:

c = WorldData[World[[113]]]; t = Table[StringJoin["t", ToString[i]], {i, 1, Length[c]}]; Do[ t[[i]] = Transpose[{-First[Transpose[c[[i]]]], Last[Transpose[c[[i]]]] - Sign[Last[Transpose[c[[i]]] - .1]]*10800}], {i, 1, Length[c]}]; t

{{{2501, -359}, {2430, -437}, {2505, -512}, {2773, -796}, {2753, -553}, {2685, -571}, {2634, -468}, {2598, -543}, {2596, -435}, {2501, -359}}, {{2381, -184}, {2497, -286}, {2412, -279}, {2365, -372}, {2224, -303}, {2065, -438}, {2258, -240}, {2262, -87}, {2381, -184}}}

We can now add this data to WorldData.m in the Miscellaneous StandardPackages under the name "~New Zealand" and add that name to the WorldNames.m document. After restarting Mathematica...

WorldPlot[{{"New Zealand"}, RandomColors}, WorldBackground -> Gray]

WorldPlot[{{"~New Zealand"}, RandomColors}, WorldBackground -> Gray]

Where In The World...?

Of course, this gives us absolutely no clue as to where the antipodal map overlaps reality...

WorldPlot[{{"Morocco", "Spain", "Portugal", "Italy"}, RandomColors}, WorldBackground -> Gray]

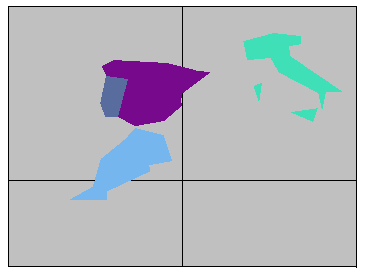
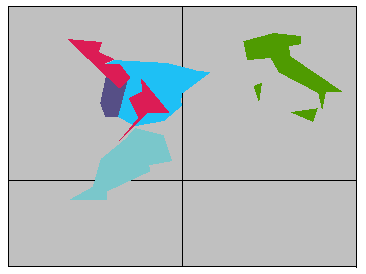
WorldPlot[{{"Morocco", "Spain", "Portugal", "Italy", "~New Zealand"}, RandomColors}, WorldBackground -> Gray]

So, Antipodal New Zealand (in red, above right) lies at the same north latitude as Italy, but is closer to - and on the other side of - the prime meridian. It intersects both Portugal and Spain and - in this representation - misses Morocco.

Now, what we did with New Zealand can be done with any other country. Better still, we can do it with all countries...

Table[StringJoin["\"~", World[[j]], "\""], {j, 1, Length[World]}]

Do[c = WorldData[World[[j]]]; t = Table[StringJoin["t", ToString[i]], {i, 1, Length[c]}]; Do[t[[i]] = Transpose[{-First[Transpose[c[[i]]]], Last[Transpose[c[[i]]]] - Sign[Last[Transpose[c[[i]]] - .1]]*10800}], {i, 1, Length[c]}]; Print[StringJoin["WorldData/: WorldData[\"~", World[[j]], "\"] = ", ToString[t]]], {j, 1, Length[World]}]

This gives us a list of antipodal countries (to be added to WorldNames.m) and a printout of their corresponding data points (to be added to WorldData.m). One caveat: Antipodal United Kingdom wouldn't plot for me until I changed its two 10800 latitudes to 10799.

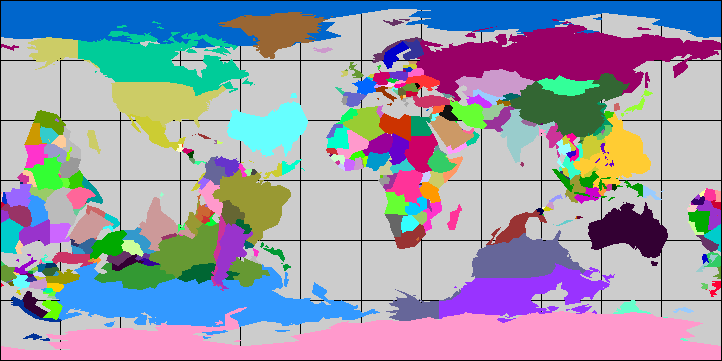
Antipodal World

WorldPlot[{World, RandomColors}, WorldBackground -> Gray]

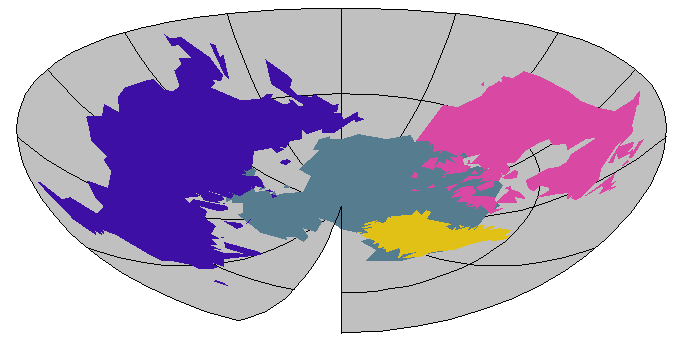
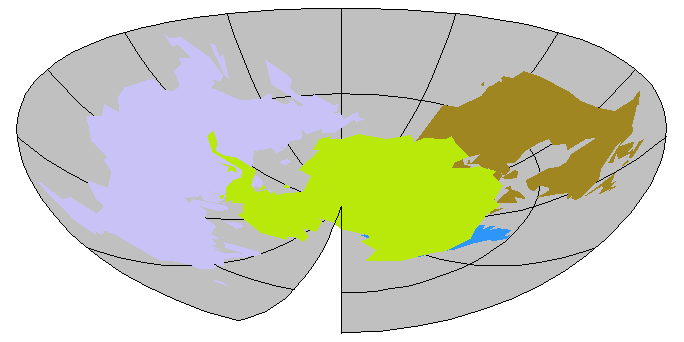
Antarctica

WorldPlot[{{"Antarctica", "~Canada", "~Greenland", "~Russia"}, RandomColors}, WorldBackground -> Gray, WorldProjection -> LambertAzimuthal]

WorldPlot[{{"~Canada", "~Greenland", "~Russia", "Antarctica"}, RandomColors}, WorldBackground -> Gray, WorldProjection -> LambertAzimuthal]

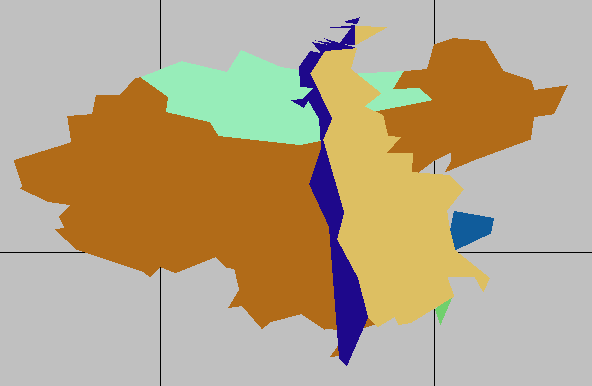
China

WorldPlot[{{"China", "Taiwan", "Mongolia", "~Uruguay", "~Argentina", "~Chile"}, RandomColors}, WorldBackground -> Gray]

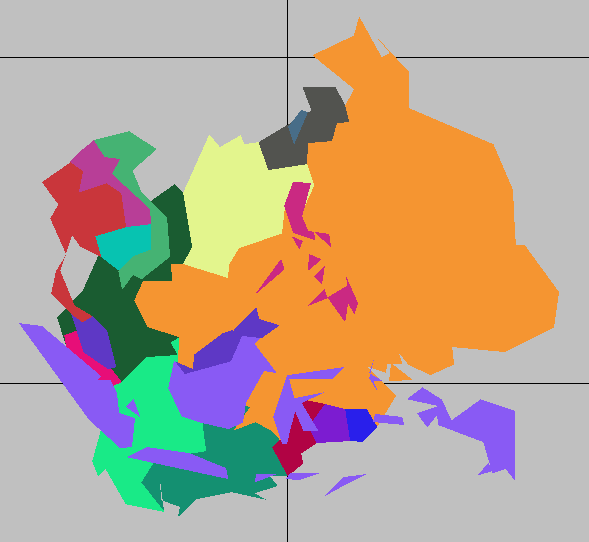
South of China

WorldPlot[{{"~Brazil", "~Peru", "~Colombia", "~Bolivia", "~Paraguay", "~Ecuador", "~Venezuela", "~Guyana", "~Suriname", "~French Guiana", "Laos", "Cambodia", "Vietnam", "Thailand", "Malaysia", "Indonesia", "Taiwan", "Philippines"}, RandomColors}, WorldBackground -> Gray]