Four-Part Harmony

Computing π in seahorse valley
Back in 1991, Dave Boll noticed that the decimal digits of π were coming up as the number of iterations required for the neck of the Mandelbrot set to escape a circle of radius two, using successive negative powers of ten as the imaginary coefficient of the constant c = -3/4 + x i in the transform z = z^2 + c, initial z = 0.
Boll's eight terms were used in Aaron Klebanoff's proof of the observation and in Gerald McGarvey's submission, in 2004, to Sloane's OEIS. Four weeks ago, Robert Munafo discovered that the eighth term was out by one. He then calculated an additional five terms.
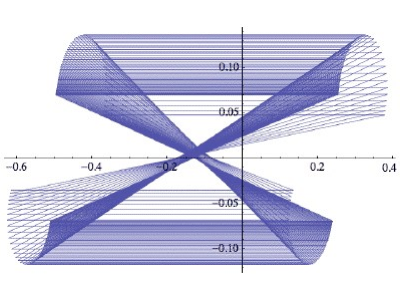
I got involved at this point — trying to verify the sequence extension in Mathematica, which I was able to accomplish for all but the final two terms. In the process, I decided to investigate how sundry start-values escape the radius-two circle (in the complex plane) and came up with this helpful illustration. The proximity of the escape points for x=10^-3 and x=10^-9 (at the top of the picture) had Robert Munafo note that in the decimal digits of π (3.14159265358979...), the three digits after the third and after the ninth decimal place (shown in red) were also close. He suggested that there was "almost certainly" a connection.
Thus began on my part an intense effort to understand the nature of the escape-point function for the given transform. For z = z^2 + c (initial z = 0, c = -3/4 + i/n), I drew graphs of the escape-point 'orbits' for positive reals, beginning at n=0 and proceeding to infinity. It appears that from n=164.2 on, the orbits (each consisting of two distinct curve segments) approach a limit-graph with a period of 2/π. I subsequently drew that limit-orbit (using a reference orbit at n=10^6) and superimposed nine powers-of-ten escape points, each with its final four-iteration escape trajectory.
Escape points for n=a and n=b will be nearby if π*(b-a)/2 is close to an integer. The property of Robert Munafo's close-three-digits in the decimal-digits of π can be shown, on the other hand, to follow from π*(b-a) being close to an integer. Half of these will have π*(b-a)/2 close to an integer plus 1/2. Therefore, reversing the process to discover nearby escape points by noting close coincidences in π's decimal digits will only work, on average, half of the time.
Wednesday, February 3, 2010